The environment contains all of the objects and properties to define your virtual environment. This includes a list of all organisms and structures, and the ground and water surfaces.
It is also where you configure global properties like the magnitude of gravity.
Virtual Environment Properties
Mouse Spring Settings
When a simulation is run the user can grab pieces in the simulation to try and
manipulate them. When the user holds down the shift and control keys and clicks on
a rigid body using the left mouse button a spring is attached to the rigid body
from the point where the initial click occured to the end of the mouse pointer.
By moving the pointer you can stretch the spring to apply forces to the rigid body
at the selected point. These two properties control the springs behavior.
This sets the damping of the spring. In other words, this controls how
quickly the force is applied for a given change in length.
Default value: 200 g/s
Acceptable range: Any value greater than 0.
This sets the stiffness of the spring. This is how much force is to be applied for a given change in length.
If you increase this value then your mouse spring can apply more force using smaller movements. However,
you need to be careful here because if you apply forces that are too large you will rip the parts away from
their joints and cause the simulation to become unstable.
Default value: 0.5 N/m
Acceptable range: Any value greater than 0.
Settings
This is the magnitude of gravity. It is applied along the Y axis. If you want your simulation to take place in a weightless environment then set this value to zero.
Default value:-9.8 m/s
2
Acceptable range: Any value.
This is the time step for the physics engine. This is one of the most important properties for producing a stable simulation.
It is imperitave that you set this appropriately. If your simulation uses small distance or mass units or large forces then
you will need to reduce the time step to allow it to run stably.
Default value: 0.5 ms
Acceptable range: Any value greater than 0.
Simulate Hydrodynamics
If this property is true then hydrodynamics are simulated. If this value is false then no hydrodynamics are simulated. This value will be set to true automatically when you add a fluid plane to the simulation.
Default value: False
Acceptable range: True/False
Units
Another important way of making sure you simulation remains stable is to use the correct mass and distance units. The magnitude of the units for
for all of you rigid bodies should remain be 0.01 and 100 in order to remain stable. For example, lets say you are simulating a grasshopper. They are
around 5-6 cm long and have parts as small as 0.1 cm or so. The weight for parts ranges from 2.3 grams to 1.5 milligrams. So in this case we
would probably use centimeters for our distance units and decigrams for our weight units. If on the other hand we were simulating a mobile robot
we might decide to use meters and decigrams. You want the biggest units that will meet your needs and keep you within the 0.01-100 range that was mentioned.
The reason for this is that if there is a wide variation in masses or sizes between objects in the simulation it can lead to instabilities that cause large
forces to be applied which cause things to blow up spectacularly. You want the largest units you can get though because the lower the unit values you use the
slower your simulation will run. This is because the forces and everything else have to be scaled up proportionally at the same time. AnimatLab uses abstract
distance and mass units internally. When you tell it to use centimeters then 1 unit = 1 cm. In this case though gravity would be -980 cm/s. So now in 1 second
a block that would have moved 1 unit in a second will move many units in that same time. To deal with this you must decrease the physics time step.
This is the distance units for this simulation.
Default value: Centimeters
Acceptable range: Kilometers, Centameters, Decameters, Meters, Decimeters, Centimeters, Millimeters
This is the mass units for this simulation.
Default value: Grams
Acceptable range: Kilograms, Centagrams, Decagrams, Grams, Decigrams, Centigrams, Milligrams
Selected Vertex Radius
The radius of the sphere used to show the selected vertex while in receptive field mode.
Default value: 5 mm
Acceptable range: Any value greater than 0.
World Stability
Constraints in Animatlab are equivalent to very stiff, strongly damped, spring damper
systems for the case position constraints, and highly dissipative viscous drags for
velocity constraints. Stiffness and damping coefficients of these potentials and dissipation
functions are adjustable by the user. The physics integrator was designed
to handle very large stiffness and damping so constraints can be made almost perfectly
rigid in most cases without having to worry much about stability.
But this leaves a few parameters controlling the overall stability and efficiency
of the solver for the user to adjust namely, compliance and damping rate of position
constraints, and the kinetic loss of velocity constraints. We now explain what
these parameters mean and how to adjust them to produce a stable and efficient
simulation.
Mechanical compliance is the ability of an object to yield elastically when a force is
applied to it. Numerically, a compliance is the inverse of a stiffness. So, with zero
compliance, constraints do not yield at all, and they become increasingly elastic
with increasing compliance.
Now, the problem with systems of noncompliant constraints is that they can
be degenerate, i.e., redundant or over defined, and solving such systems is more
difficult and therefore slower than solving for systems which are known or assumed
to be non-degenerate. What’s a degenerate system? Think of a table with four leg
on a perfectly planar floor. You know that you can remove a leg without the table
tipping over so one of the contact constraint with the floor is redundant and so the
system is degenerate. Degenerate systems are very common–especially in cases
where you have stacks and piles of objects–and AnimatLab was designed to process
these easily and seamlessly. That is why we add a small amount of constraint
compliance by default since this makes the system non-degenerate. Compliance
is both a guard against degeneracy and a modeling tool since it can be used to
relax any given constraint equation to produce a desired effect. For instance, it is
possible to turn a fixed distance constraint into a stable stiff spring. A chain of
bodies linked with compliant locked prismatic joints can be used to model a stiff
cable which has elongation, torsion and bending resistance.
Because of compliance and other reasons related to numerics, constraints are
never exactly satisfied in a AnimatLab simulation, and the constraint violations
oscillate near zero. These oscillation can be damped using a constraint damping
parameter. Without any damping, it is possible that a significant amount of the
energy of your system ends up in these oscillations which is not very good. If
damping is critical for a given compliance, you will get an optimal compromise
in stability. For damping to be critical, you need the damping ratio defined as
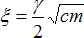
where
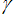
is the damping coefficient, c is the compliance, and m is the mass. This formula
applies to a simple harmonic oscillator with one point mass.
However, constraints usually involves two bodies or more, and since these attached
bodies might also be constrained to other objects in your simulation. Therefore,
computing the exact oscillation frequency and damping ratio of a given constraint
for a given compliance is not as trivial is might first appear. Indeed, this
involves computing eigenvalues of large matrices, and it is configuration dependent.
Therefore, computing critical damping coefficients is not done automatically
by AnimatLab and the user has make reasonable estimate.
To help this analysis, it is important to realize that the product of the compliance
and damping coefficient has units of time and therefore, this defines a time
scale in your system. Similarly, the ratio of compliance over squared time step has
units of inverse mass and therefore,
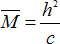
is a unit of mass (or inertial tensor)
of your system.
Now, a damping ratio of 1 means that you have critical damping and this will
prevent oscillations and force constraints to stabilize quickly. When the damping
ratio is close to 0–it is always positive–the constraints are under-damped and you
can get high frequency oscillations with high energy–even instabilities in some
cases. When the damping ratio is much larger than one, the constraint is over-damped
and this can prevent stabilization, i.e., constraints will no longer relax to a
state where they are satisfied but will remain permanently violated.
A velocity constraint is the limit case of a very strong viscous drag force, i.e., a
generalized force of the form
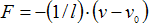
, where v is the current velocity,
v
0 is a target velocity. and l > 0 is the kinetic loss, i.e., the inverse of a viscous
drag. In the limit where l goes to 0 (the viscous drag going to infinity), the system
will satisfy the constraint v = v
0. Just like in the case of position constraint, we
force l > 0 to avoid dealing with degenerate cases. The kinetic loss is proportional
to time it takes to ramp up to the target velocity. When l is large, the system is
sluggish and when it is small, it is very prompt.
Angular and linear degrees of freedom are scaled differently and this is why
the full set of parameters are defined using the following properties
The compliance value of the spring used in angular collisions within the simulator.
Default value:0.1 um/N
Acceptable range: Any value greater than 0.
The damping value of the spring used in angular collisions within the simulator.
Default value:50 Kg/s
Acceptable range: Any value greater than 0.
The amount of kinetic loss for angular collisions within the simulator.
Default value:1 ug/s
Acceptable range: Any value greater than 0.
The compliance value of the spring used in linear collisions within the simulator.
Default value:0.1 um/N
Acceptable range: Any value greater than 0.
The damping value of the spring used in linear collisions within the simulator.
Default value:200 Kg/s
Acceptable range: Any value greater than 0.
The amount of kinetic loss for linear collisions within the simulator.
Default value:1 ug/s
Acceptable range: Any value greater than 0.
By default, compliance and kinetic loss are all near 10E-12 in double precision
and 10E-4 in single precision. The damping coefficients are 10E10. This is small
enough to make constraints almost rigid but can cause problems if the masses in
your systems are big enough.
To understand the relation between these parameters and your system, the thing
to observe is that linear compliance has the units of the inverse a spring constant
and for a linear variable, these are: squared time over mass. The perturbation added
to the system matrix, which has units of inverse mass, is
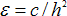
where c is the
compliance, and h is the time step. Now, if e is much smaller than the inverse of
the biggest mass in your system, it is then very close to 0 and will therefore have
practically no influence on the overall dynamics.
As soon as you have masses large enough such such that e is comparable to
the inverse, your system will be more compliant. This might be the effect you
are looking for. Decreasing compliance will work up to a point where your system
matrix is found to be singular or nearly so. At that point, your simulations will slow
down because the LCP solver has a harder time finding solutions, and eventually,
the matrix factorizer will detect that your matrices are no longer positive definite
and this causes a fatal error.
The choosing the damping coefficients is not automated yet and sometimes require
attention. To produce critical damping on a linear mode, one must know the mass
of that mode. To see this, consider the simple damped harmonic oscillator:
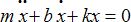
, where m is the mass, b the damping coefficient, and k the spring
constant. This spring is critically damped when
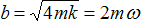
, where
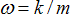
is the natural frequency of the spring. The problem here is that it’s not clear what
is the mass attached to one constraint. For instance, if you have a chain fixed on
the ceiling with several links of mass m, and a load of mass M, the mass on each
constraint will be close to M when the chain is at rest, pointing downward, and
closer to m when horizontal. So, you cannot tell how to fix critical damping for all
cases.
If damping is too high, the constraints will not relax back to zero violation and
if there is insufficient damping, you might find instability.